こんにちは、蔓迷路です。

以前の記事で「学習計画は“内容”ではなく“成果”をまずは考えよう」という趣旨の話を書きました。

このように成果ベースで考えるとき、区切り良く扱える1つの単位として、「単元」という区分があります。

今回は皆さんのそういったテーマごとの学習が捗るよう、物理の一単元である「単振動」のワンポイントをまとめてみようと思いました。

理系物理選択の皆さんは是非、スキマ時間にご活用ください！

力学の基本・時間微分

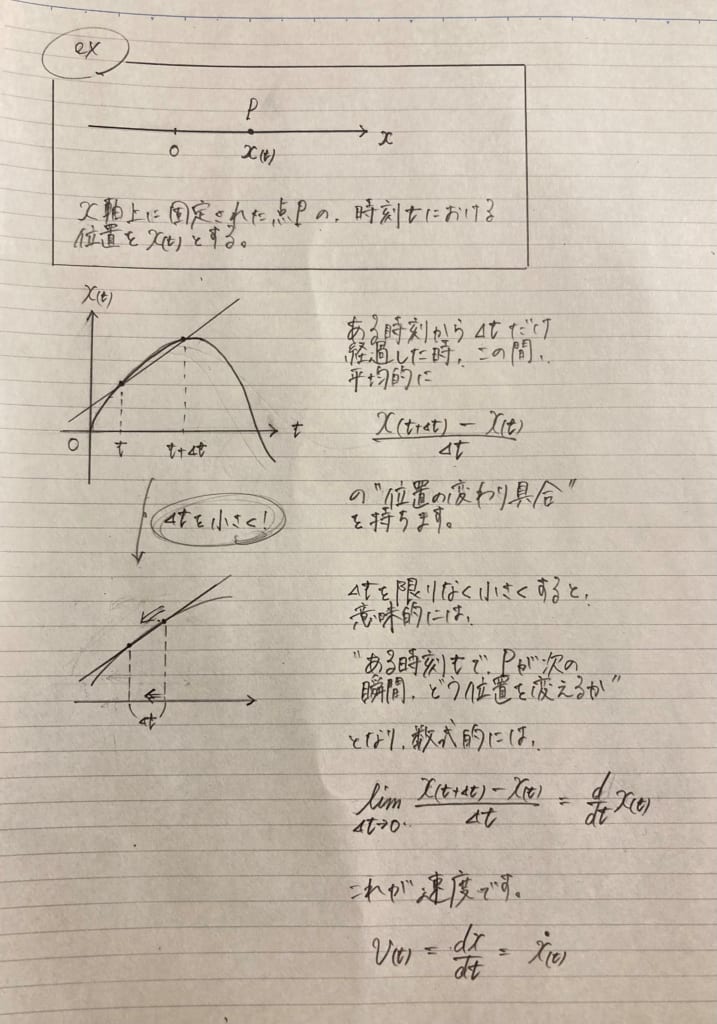
皆さんが意識しているかはわかりませんが、速度は位置の時間微分、加速度は速度の時間微分です。

「え、急になんで？」と言われても、「それはもうそれが定義だからね」という話になってしまいます。

多くの高校では基本的に微分積分を物理に持ち込みませんよね。これは数学Ⅲを履修しない物理選択者でも話についていけるようにしているのです。

しかし、この記事ではその一線は超えて、本来的な意味から理解してもらおうと思います！

先ほどは定義だからと言って軽く流しましたが、一応イメージを説明しておくと、「ある時刻において、次の瞬間にどんな移動をしようとしているか」が位置の時間微分であり、速度です。なんとなく伝わりますかね？

同様に考えて加速度は速度の時間微分なので、加速度は「位置の微分」の微分、つまり位置の関数を時間で二階微分したものが加速度になりますね。これをまず前提とします。

単振動の式

ではいよいよ、単振動の式を書きます。

時間の関数を用いて、位置の関数をsinで書ける現象こそが単振動です。

結果として、「加速度＝負の定数×位置」を一般的に得られましたが、この式がどんな意味を持つでしょうか？ちょっと考えてみてください。

例えば、位置が正の方に大きくなればなるほど、加速度は負の方に大きくなります。また、その逆も然りで、位置が負に大きければ加速度は正に大きくなります。

こうして、この式はｘ＝０に戻ろうと、左右に行ったり来たりする運動を表していると解釈できると思います。

基本的な例題で確認

では、ばね定数ｋのばねに吊るされた質量ｍの小球の運動で式を立て、実際にイメージしながら式を眺めてみましょう！

この問題では、ｘ＝ｍｇ/ｋ、つまり釣り合いの位置に戻ろうとする運動であることが分かりますね！

このように、運動方程式を書けば振動中心と角振動数（およびその逆数に2πを掛けた周期）が分かります。

これで単振動の式はＯＫ！

運動方程式を立てた時に「加速度＝負の定数×位置」を得たら単振動と分かり、振動中心と角振動数を求められるようになればＯＫです！

お手持ちの教材の簡単な例で構いません、ぜひ自分の手で立式してみてください！

蔓迷路

早稲田大学 教育学部

この記事が気に入ったら
いいね！して応援しよう！

16+